5.1.6. A normális eloszlás

Térjünk most vissza a pénzfeldobáshoz. Az ξ változó szórása:

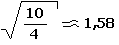
A változó lehetséges értékeinek valószínűségeit a következő diagramon ábrázolhatjuk:

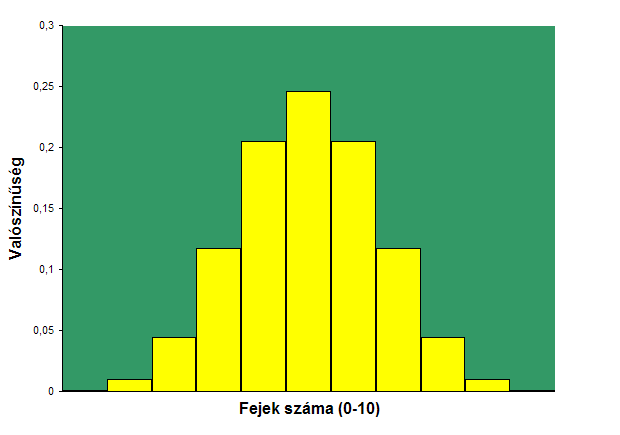
Ha a valószínűségek elméleti kiszámítása helyett sokszor elvégezzük a tízes dobássorozatot, és az egyes eredmények relatív gyakoriságát ábrázoljuk ugyanígy készített diagramon, akkor várhatóan minél több sorozatot dobunk, annál hasonlóbb lesz az ábra a fentihez. Ha tízes helyett százas dobássorozatokat vizsgáljuk, ugyancsak azt látjuk, hogy a valószínűségek a várható érték környékén a legnagyobbak, úgy, hogy a várható érték egy környezetében viszonylag nagyok a valószínűségek, aztán mindkét irányban gyorsan fogyásnak indulnak. Ennek a környezetnek a nagyságát méri a szórás. Nyomjuk össze a százas sorozatok valószínűségeinek ugyanígy elkészített diagramját ugyanerre a szélességre. A következőt látjuk:

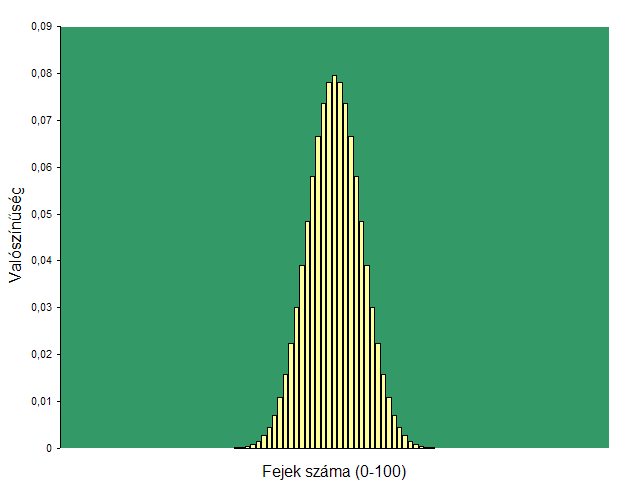
A fejek számát mutató vízszintes tengely jóval kisebb részén sűrűsödnek azok a valószínűség-értékek, amelyek egyáltalán láthatók. (Természetesen a harminc, vagy akár az egyetlen fejet tartalmazó sorozatoknak is van valamilyen valószínűsége, de olyan kicsi, hogy eltűnik az ábrán.) Az egész ábra pedig egy jellegzetes harangalakot formáz, ami jó ismerőse mindenkinek, aki akár csak futólag is foglalkozott valaha statisztikákkal. Ha még tovább növelnénk a sorozatok hosszát, még közelebb jutnánk a Gauss- vagy haranggörbéhez. Ez egy exponenciális egyenlettel leírható görbe, amit két paraméter határoz meg: az egyik a maximumának (szimmetriatengelyének) helye, a másik egy olyan számérték, amely a harang "szélességét" adja meg (nem a pontos geometriai értelemben vett szélességet, mert az végtelen, hanem annak a sávnak a szélességét, amelyen belül még viszonylag nagy függvényértékek találhatók). Ez a két paraméter nem más, mint a várható érték és a szórás. A Gauss-görbének megfelelően viselkedő változókat normális eloszlású valószínűségi változóknak nevezzük.

A valószínűségszámítás egy fontos tétele, a centrális határeloszlás-tétel lényegében azt mondja ki, hogy független és egyformán viselkedő valószínűségi változók összege az összeadandók számának növelésével a gyakorlatban általában teljesülő feltételek mellett, a normális eloszláshoz tart, azaz az összeg ábrája a Gauss-görbét közelíti. Tehát ha egy kísérletet sokszor végzünk el azonos körülmények között, vagy statisztikai úton olyan mennyiségeket figyelünk meg sok példányban, amelyek azonos módon függnek a véletlentől, azt várhatjuk, hogy az eredmények a Gauss-görbe által szemléltetett módon fognak ingadozni a várható érték körül. A szórás ismeretében ennél lényegesen többet is lehet mondani: az várható, hogy a várható értéktől a szórásnál kevesebbel fog eltérni az eredmények 0,68, a szórás kétszeresénél kevesebbel 0,97, a szórás háromszorosánál kevesebbel 0,997 része. A legutóbbi diagramon ábrázolt, százas fej vagy írás-sorozatokat leíró valószínűségi változó szórása 5, tehát a harmincötnél kevesebb vagy hatvanötnél több fejet tartalmazó sorozatok várható aránya kevesebb, mint három ezrelék (nem csoda, ha nem látszanak az ábrán). Iktassunk ide egy Gauss-görbét. Az ábrázolt, normális eloszlású valószínűségi változó várható értéke legyen 50, a szórása 2, az ábrán elég lesz a 40 és 60 közötti értékeket ábrázolni. Most azonban bonyolultabb lenne pontosan megmondani, mi a jelentése a függőleges tengelyen levő számoknak. Lényegében és leegyszerűsítve arról van szó, hogy a fenti két diagramot is át kellene értelmeznünk: valójában nem az oszlopok magassága, hanem a területük tekinthető az egyes értékekhez tartozó valószínűségek ábrázolásának. Most annak a valószínűségét, hogy a változónk értéke a vízszintes tengelyen levő két pont közé essen, a görbe megfelelő szakasza alá eső terület jeleníti meg, a görbéről pedig azt mondhatjuk, hogy a változó eloszlásának sűrűségét ábrázolja:

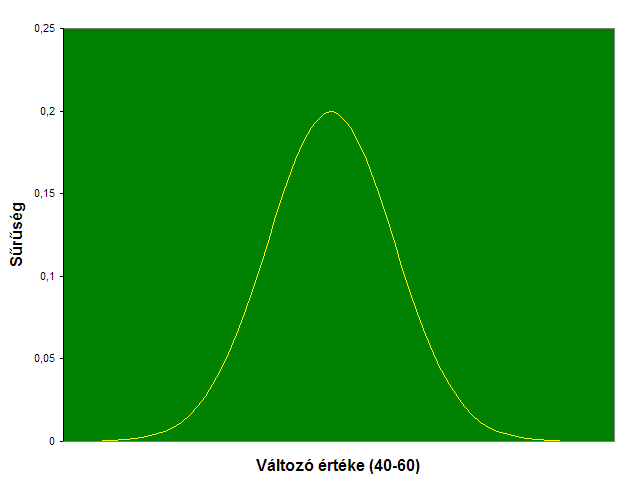
A centrális határeloszlás-tétel ismeretében tehát tudhatjuk: nem volt semmi jelentősége, hogy olyan egyszerűen viselkedő valószínűségi változókat összegeztünk, mint az egyetlen pénzfeldobást leíró változók. Ha mondjuk egy népesség minden azonos korú és nemű tagjának hátralevő élettartamát egy-egy valószínűségi változónak tekintjük, ezek értéke a Gauss-görbe szerint kell, hogy ingadozzon az átlagos hátralevő élettartam körül - feltéve, hogy az illetőknek tényleg azonos az esélyük arra, hogy egy, két, három ... évet éljenek még. De ez már következő fejezetünkbe, a statisztikával kapcsolatos kérdésekhez tartozik.